今天全是原题,然而窝几乎都没做过,于是挂了……
丢人的是考场上组合数的式子 $C[i][j]$=$C[i$-$1][j]$+$C[i$-$1][j$-$1]$ 写成了 $C[i][j]$=$C[i][j$-$1]$+$C[i$-$1][j$-$1]$ ,然后第一题光荣爆 $0$ ……TAT。
吸取教训!
题目压缩包戳我!!!~\(≧▽≦)/~(有时链接可能会崩,如果崩了的话请稍后尝试QwQ)
T1
期望得分:100分
实际得分:0分
正解:Purfer+DP+组合数学
窝的解法:Purfer+DP+组合数学
题解:
十年OI一场空,组合数打错见祖宗。
上面的正解有误,听说 $DP$ 不是正解,不过,$DP$ 复杂度高达 $O(n^4)$ ,本应该 $T$ 的,却仗着小常数不仅 $AC$ ,还爆踩标程?这究竟是道德的沦丧还是人性的扭曲?
不了不了,正经一点。众所周知,有个东西叫 $Purfer$ 序列,对于每一个不同的树,都有不同的 $Purfer$ 序列。所以每个树都可以用其 $Purfer$ 序列来表示,这个树中的每个结点在 $Purfer$ 序列中的出现次数为其度数减一。至于$Purfer$ 序列具体是什么就不赘述了。
那么 $DP$ 方程怎么设?
我们设 $f[i][j][k]$ 表示 从前 $i$ 个结点中选出 $j$ 个结点,并且这 $j$ 个结点共在原树的 $Purfer$ 序列出现了 $k$ 次的合法 $Purfer$ 序列的数量 。
那么转移呢?很显然分为两种情况:
- 没选第 $i$ 个点。
- 选了第 $i$ 个点。
然后分别进行转移,这就很简单了:
- 没选:$f[i][j][k]+=f[i-1][j][k]$
- 选了:$f[i][j][k]+=f[i-1][j-1][k-d]\times C[k][d]$
其中 $d$ 为我们正在枚举的第 $i$ 个点的出现次数 $(0$ ~ $du[i]-1)$ ,然后就是下面的组合数,就是代表着在 $k-d$ 长度的序列中插入 $d$ 个 $i$ 的方案数 。
当然也可以这么写:
我们知道一棵 $n$ 个结点的树的 $Purfer$ 序列的长度是 $n-2$ 的,所以我们的答案应该就是 $f[n][i][i-2]$ 。
最后,记得随时膜模!
Code:
1 |
|
T2
期望得分:5分
实际得分:30分
正解:???没发sol……
窝的解法:手玩小数据+瞎搞
题解:
一看就是懵逼题……但是看到 $30$ 分的数据很小,并且还有菊花图,所以我们来瞎搞吧!刚开始的时候以为前六个点都是菊花图,然后都手玩,到后面才看清,只能说数据太弱了啊。
正解表示不明白……贴一发考场上的代码:
Code:
1 |
|
实际上玩到 $n$=$5\&\&k$=$2$ 的时候我就崩了,玩不下去了。
T3
期望得分:0分
实际得分:0分
正解:最小割
窝的解法:没做….
题解:
真的看不出来是最小割啊 $QwQ$ ,以为是数论题,还看到质因子了感觉就更不像最小割了……但是在想题目的时候最小割的确出现在了我的脑海中,但是一闪就过了……
一个有趣的事情:考试期间高二机房神仙一度怀疑此题为数论题,这个时候 $chl$神仙 和另一位 $Dalao$ 走了出去,站在门外讨论此题中的”物理”,说什么重心和”物理”有关因此此题不可做,然后树王神仙表示不懂”物理”中的”重心”准备弃疗,然而最终树王神仙还是选择了网络流……
好吧不扯淡了,我们来讨论一下这题的粗略解法。
可以发现题目给出了一个限制:$N$ 最多有两个质因子。这个限制有什么用呢?
对于一个有 $N$ 个扇叶的风扇,我们考虑平衡的并且独立扇叶只有一个的风扇:
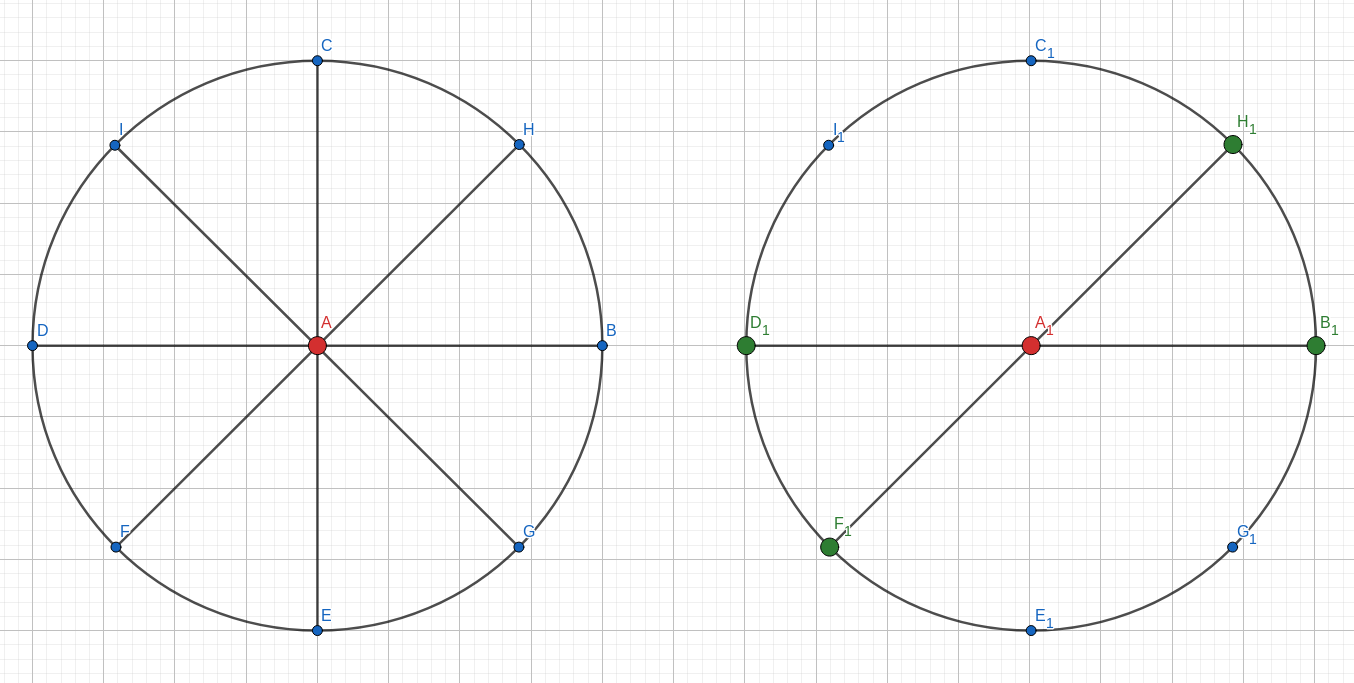
左边的就是有 $(N=8)$ 个扇叶的风扇,右边的呢就是在 $8$ 个扇叶中有 $2$ 个扇叶的风扇 ($(A_1,D_1,F_1),$$(A_1,H_1,B_1)$),可以知道这个 $2$ 个扇叶的风扇是一定平衡的,因为 $2$ 是 $8$ 的因子。
可以知道,对于 $8$ 的其他因子(例如 $4$ )是可以被质因子 $2$ 组成的,因此也是平衡的风扇。
那么对于两个不同的质因子,可以组成两个不同样式的且平衡的 $N$ 个扇叶的风扇的子风扇。
当然还有位置不同,对于上图中 $2$ 个扇叶的子风扇根据不同的位置有很多个:
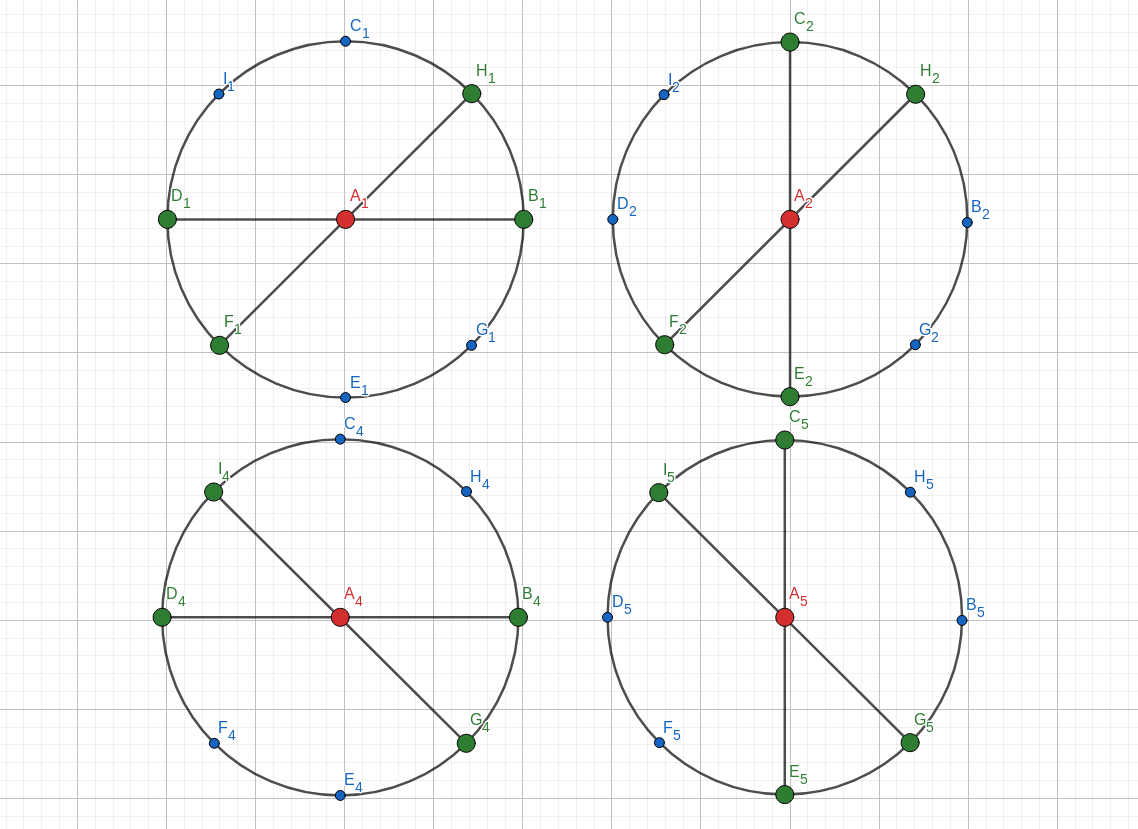
这个时候我们的问题就可以转化如下了:
有两种类型的风扇 $p,q$ ,风扇类型等于 $2$ 的样子如上图,现在我们需要用这两种风扇无重叠的覆盖尽可能多的剩下的残缺扇叶。
这个时候考虑建图,我们从 $S$ 向所有不同位置的 $p$ 类风扇连一条边,边权为 $p$ ,表示选择了这个风扇可以多覆盖一共 $p$ 个扇叶。所有不同位置的 $q$ 类风扇向 $T$ 连边,边权为 $q$ ,和上面同理。
然后这个时候的最小割是什么呢?对于一个起点为 $x$ 的 $p$ 类风扇,我们将 $S$ 连向Ta的边切断,表示不使用起点为 $x$ 的 $p$ 类风扇,$q$ 类风扇同理。当然是不使用的风扇越少越好,剩下的可用的风扇当然是越多越好,所以成了最小割。
那么怎么表示无重叠呢?
可以知道同类风扇是不可能重叠的,我们考虑异类风扇。我们对于一个 $p$ 类风扇和一个 $q$ 类风扇,如果其重叠了,那么只能选择其中一个,于是我们在这两个风扇间连一条边,边权为 $inf$ ,这个时候跑最大流的时候必定有流经过此地,也就是说这两个风扇必然要割掉一个才行。
所以什么事情都解决了,就差代码了。
Code:
1 |
|
本文标题:【考试总结】 Test-2019.3.27 HNOI2019模拟
文章作者:Qiuly
发布时间:2019年03月27日 - 00:00
最后更新:2019年04月03日 - 17:32
原始链接:http://qiulyblog.github.io/2019/03/27/[考试总结]test20190327/
许可协议: 署名-非商业性使用-禁止演绎 4.0 国际 转载请保留原文链接及作者。